路遙知碼力,日久練成精- 只要在程式之路鑽研的夠深,便能夠充分發揮程式碼的力量; 練習的日子夠久,便能夠練成寫出精簡代碼的能力。
我們經歷了自定函數技巧、遞迴黑魔法的淬鍊後,
要為大家介紹第二個程式小專題囉。
(看此篇之前,建議先看過昨天對遞迴函數的介紹)
這次的問題也是個經典問題,
八皇后問題是西洋棋延伸而來的問題,
西洋棋的皇后是威力很大的棋子,
皇后在棋盤上的「攻擊範圍」為同行、同列、同對角線的地方,
要如何在8*8的方形棋盤上擺放八個皇后,使得每個皇后互相不在攻擊範圍中?
希望以程式找出所有不同的解。
當然,我們可以將問題推廣為:
「如何在n*n的方形棋盤上擺放n個皇后,使得每個皇后互相不在攻擊範圍中?」。
考量或許不是每個人都玩過西洋棋,
這邊我畫個簡單的示意圖描述什麼是皇后的「攻擊範圍」: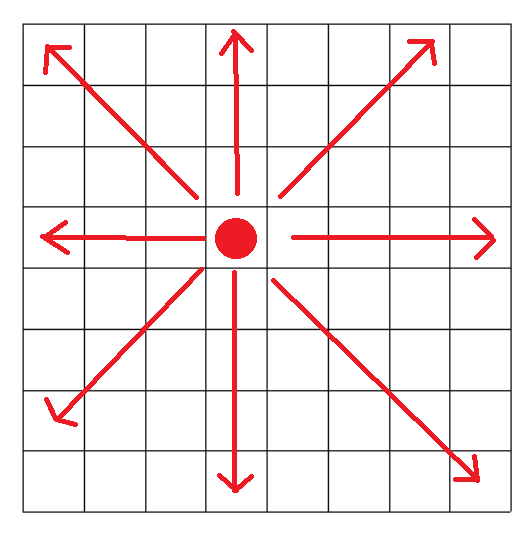
如圖示,假設以紅點代表皇后,
那麼由該點延伸出去同行、同列、同對角線都是不能放皇后的。
給出一組八皇后問題的範例解: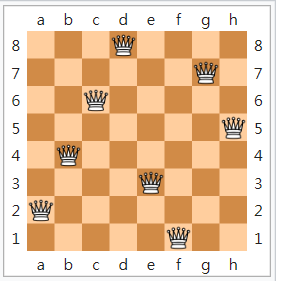
(圖片來源: 維基百科)
該如何思考解題呢?
為了方便思考,先從小case四皇后問題想起吧
在正式解問題之前,首先我們先決定如何表示一組解答,
最直覺的方式恐怕是用一個二維列表在表示整個棋盤吧,
以0表示沒有放皇后,1表示有放皇后,
比如說用
[[0, 1, 0, 0],
[0, 0, 0, 1],
[1, 0, 0, 0],
[0, 0, 1, 0],]
表示一組放皇后的格式,
這樣子最符合直覺,
可是我們發現,因為棋盤大部分的格子是不擺皇后的,
這樣記錄一組解其實蠻浪費空間的。
我們可以確定,
至少我們不會傻到在同一列放上兩個皇后,
所以實際上我們每列用一個數字用可以記錄皇后放在哪個位置了,
在上例中,皇后放在
第一列index 1 的位置,
第二列index 3 的位置,
第三列index 0 的位置,
第四列index 2 的位置,
因此,我們可以簡單用元組(1,3,0,2)來表示這組解。
整個問題的思考主軸大概就是建立如何擺放皇后的遞迴關係了。
我們會想要一列一列擺放皇后,
第一列皇后位置擺好後嘗試在第二列放皇后。
假設我們有一個神奇的函數queens(n, state),n代表總共有幾個皇后,state以元組代表前已經擺好的皇后位置,
然後這個函數會回傳後續所有可能的解。
譬如我們可以窮舉知道四皇后問題只有(1,3,0,2),(2,0,3,1)這兩組解。
(注意: 當python元組(tuple)只有一個元素,應該寫(1,)而非(1))
我們期待,當我們呼叫queens(4, (1,))這個函數時,
會返回[(3,0,2)],把後續可能的皇后位置以列表形式回傳。
試想,如果queens(n, state)有這樣的效果,
那我們只要呼叫queens(4, ())便可以得到[(1,3,0,2), (2,0,3,1)]所有答案了。
那麼該如何寫遞迴關係呢?
假設我們已經在第一列的index0的位置放了一個皇后: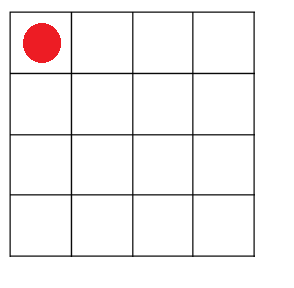
那麼扣除「攻擊範圍」,第二列可放的index就只有2跟3了,如圖示: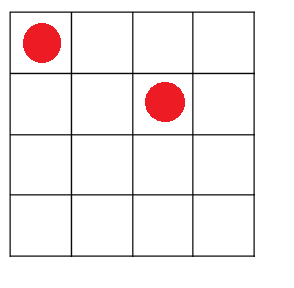
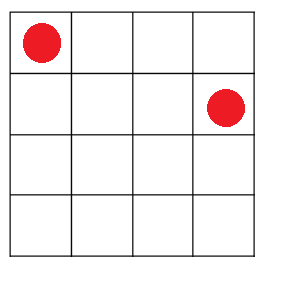
仔細想想,queens(4, (0,))的所有解,不是能夠由queens(4, (0,2))的queens(4, (0,3))的所有解給拼湊出來嗎?
我們試著給程式邏輯打個草稿吧:
def queens(n, state):
ans = [] #記錄在state棋子已經放好的狀況下,後續的所有解答
for 位置 in range(n): #嘗試在下一列中放新的皇后
if 這個位置不在前面皇后的攻擊範圍:
ans 添加所有來自queens(n, state+(位置, ))的解答
return ans
嗯…邏輯大概就是這樣,接著我們把細節想的更清楚一些。
由於我們希望判斷下一列中放新的皇后會不會在前面皇后的攻擊範圍,
我們定義一個這樣的函數conflict(state, nextX),
若新皇后在任何已放置皇后的攻擊範圍,回傳True。
比如說conflict((0,), 1)的意思是,
假設我們已經在第一列index0放了一個皇后,
再下一列index1的位置放皇后有沒有事?如圖示: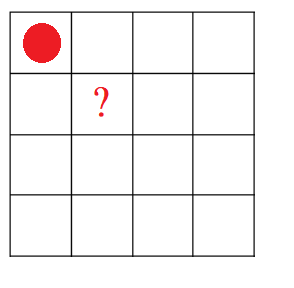
(以本例來說,此皇后在第一個皇后的斜對角攻擊範圍,應回傳True)
大家可以自行做簡單數學推導,
若兩組(x,y)座標在同一條對角線,
x座標絕對值之差 = y座標絕對值之差。
我們的邏輯就判斷兩件事:
True
True
其餘狀況都返回False,
搭配Day17我們教過的any函數,
函數可以這樣實作:
def conflict(state, nextX):
nextY = len(state)
if any(abs(state[i] - nextX)== 0 for i in range(len(state))): #同行
return True
if any(abs(state[i] - nextX)== nextY - i for i in range(len(state))): #同對角線
return True
return False
另外,判斷同行與同對角線的邏輯類似,
我們可以再次精簡函數:
def conflict(state, nextX):
nextY = len(state)
return any(abs(state[i] - nextX) in (0, nextY - i) for i in range(nextY))
精簡完成。
剛剛queens(n, state)只是簡單打了函數邏輯,
有了判斷衝突的conflict函數,我們試著補上細節:
def queens(n, state):
ans = []
for pos in range(n):
if not conflict(state, pos):
ans += [(pos,)+ result for result in queens(n, state + (pos,))]
return ans
昨天教遞迴函數時有提醒大家一定要記得設「終止條件」,
否則函數會一直呼叫下去停不下來。
那此例的終止條件,
當然就是把n個皇后放好放滿囉。
在queens(n, state)加上if len(state) == n: return [()]這個條件吧:
(注意: 是return [()]而不是return ())
def queens(n, state):
if len(state) == n:
return [()]
ans = []
for pos in range(n):
if not conflict(state, pos):
ans += [(pos,)+ result for result in queens(n, state + (pos,))]
return ans
全部大功告成了,最後呼叫一下print(queens(4,())),
應該就可以得到[(1, 3, 0, 2), (2, 0, 3, 1)]的結果囉。
如果每次我們都要呼叫函數queens(4,())似乎有點麻煩,
我們希望只要呼叫函數queens(4)即可得到四皇后問題的解答,
因此,我們可以這樣定義函數def queens(n, state=()):,
直接將state的默認值設為空元組()。
至此,我們也能夠說明為何我們傾向用元組(例如:(1,3,0,2))表達一組解,
而非用列表[1,3,0,2]表達一組解了。
基於Day20- 可變變數的災難所述原因,
這邊我們偏好以不可變變數做為默認參數。
def conflict(state, nextX):
nextY = len(state)
return any(abs(state[i] - nextX) in (0, nextY - i) for i in range(nextY))
def queens(n, state=()):
if len(state) == n:
return [()]
ans = []
for pos in range(n):
if not conflict(state, pos):
ans += [(pos,)+ result for result in queens(n, state + (pos,))]
return ans
print(queens(4))
哇,我們完成了,
看似複雜的n皇后問題,
整個函數加上印出結果只要短短十二行就解了,
今天再度將前幾天所學融會貫通的運用了,
大家感受到python魔力了嗎?
預計明天將繼續秀python魅力,解經典問題- 數獨,敬請期待。
本篇參考資料記錄了多種語言的八皇后問題解法,
但要解到如此精簡,恐怕還是對python理解要夠深啊。
給大家一個簡單的課後練習,
在本文中,我們使用一個元組如(1,3,0,2)表達一組n皇后問題的解,
然而,我們無法從(1,3,0,2)馬上反應過來皇后在棋盤上怎麼擺,
因此,我們希望可以讓程式「視覺化」的顯示皇后位置,
例如用個「.」表示空位置,「Q」表示皇后:
.Q..
...Q
Q...
..Q.
請實作一個轉換格式的函數將元組形式的答案轉為字串的列表:
def trans(state):
return
參數state是一個非空元組表示一組n皇后問題的解,
例如:
輸入: state = (1, 3, 0, 2)
輸出: ['.Q..', '...Q', 'Q...', '..Q.']
歡迎於留言區討論想法哦。

文章寫得很棒!
我也留下我的想法
我的視覺化想法是
def visualize(state):
vis=['....','....','....','....']
for i ,item in enumerate(state):
vis[i]=vis[i][:item]+"Q"+vis[i][item+1:]
return vis